Электронное пособие по теме “Функциональные последовательности и ряды"

Ответ: - область сходимости заданного функционального ряда.

Пример №6 (№18 из , студент самостоятельно у доски).

Найти область сходимости функционального ряда:

Решение

По признаку Даламбера абсолютной сходимости функционального ряда можно записать:

.

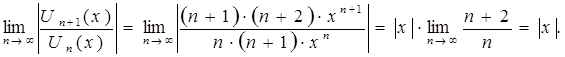Если , т.е. , то заданный функциональный ряд сходится абсолютно на интервале .

Если , т.е. , то ряд расходится.

Исследуем заданный функциональный ряд на сходимость в точках х=1 и х= - 1.

При получается числовой положительный ряд . Он является расходящимся, так как не выполняется необходимое условие сходимости числового ряда, т.е. . Значит, заданный функциональный ряд в точке расходится.

При получается числовой знакочередующийся ряд вида 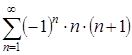. Он является расходящимся, так как не удовлетворяет условиям признака Лейбница: а) ; б) .

Ряд составленный из абсолютных величин элементов ряда имеет вид и является расходящимся.

Значит, исходный функциональный ряд расходится и в точке .

Поэтому, область сходимости заданного функционального ряда интервал - .

Ответ: .

Пример №7 (№28 из [8], студент самостоятельно у доски).

Найти область сходимости функционального ряда:

.

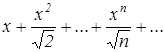Решение. Определим и заданного ряда:

, .

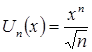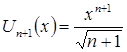По признаку Даламбера абсолютной сходимости функционального ряда имеем:

=

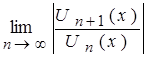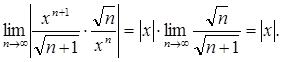
Если , т.е. , то в соответствии с признаком Даламбера абсолютной сходимости функционального ряда, исследуемый функциональный ряд сходится абсолютно на интервале .

Если , т.е. , то функциональный ряд расходится.

Исследуем заданный ряд в точках и .

Образование, педагогика, воспитание:

Осознание педагогической задачи, анализ исходных данных и постановка педагогического диагноза
В творческом процессе педагога одновременно или последовательно должны осмысливаться разные педагогические задачи. Прежде всего это должна быть общая педагогическая задача всей деятельности учителя, которая выступает как его общая концепция. Затем должна осмысливаться этапная педагогическая задача, ...

Методические рекомендации по проведению практических занятий
Концепция целенаправленного развития у студентов готовности к самообразованию приводит к тому, что самостоятельная деятельность студентов, управляемая и организуемая, тесно смыкается с образованием, которое является составной и закономерной частью целостной ситемы учебно-воспитательной работы. В ра ...

Психолингвистические требования к методике обучения английскому языку как второму иностранному
Введение второго иностранного языка в школе означает, что образование становится многоязычным: родной язык, первый иностранный, второй иностранный образуют уникальное лингвистическое явление - триглоссию. Вместе с тем, поскольку обучение любому языку неразрывно связано с культурой страны изучаемого ...