Электронное пособие по теме “Функциональные последовательности и ряды"

Если , то получается числовой положительный ряд вида . Он является расходящимся, так как , следовательно, .

Если , то элементы исходного функционального ряда меньше членов суммы бесконечно убывающей геометрической прогрессии . Для убывающей геометрической прогресси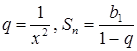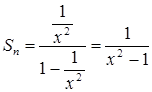и , , при .

Значит, ряд сходится при .

Следовательно, будет сходиться при и заданный функциональный ряд, т.е. областью сходимости является объединение интервалов - .

Ответ: Область сходимости заданного функционального ряда - .

Первичное закрепление материала происходит при решении студентами у доски упражнений, подобных рассмотренным с преподавателем, к доске вызываются сразу 3-4 студента.

Пример №5 (№2 из, студент у доски с помощью преподавателя).

Найти область сходимости функционального ряда:

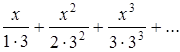
Решение

Определим формулу общего элемента заданного функционального ряда N.

По признаку Даламбера абсолютной сходимости функционального ряда имеем:

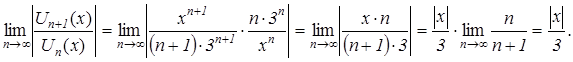
В соответствии с признаком Даламбера абсолютной сходимости функционального ряда, если , т.е. , то заданный функциональный ряд сходится абсолютно.

При , т.е. , исследуемый функциональный ряд расходится.

При x=3 функциональный ряд становится положительным числовым рядом вида . Этот ряд расходится, так как является гармоническим рядом .

При х=-3 функциональный ряд становится знакочередующимся числовым рядом вида: .

По признаку Лейбница: а) ; б) , так как .

Значит, ряд 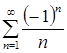сходится условно по признаку Лейбница.

Составим ряд из абсолютных величин членов ряда 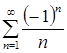. Получим ряд - это гармонический расходящийся ряд.

Значит, исходный функциональный ряд сходится абсолютно на интервале , а сходится условно на полуотрезке .

Образование, педагогика, воспитание:

Проверка результатов эксперимента
Особенно важное значение имеет проверка полученных в ходе педагогического эксперимента результатов на практике, в повседневной работе. Дело в том, что экспериментатор независимо от желания всегда находится в лучших условиях для проведения учебно-воспитательной работы, чем обычный преподаватель. Выс ...

Концепция обучения сельских школьников на основе интегративно-дифференцированного подхода
Актуальность разработанной концепции определяется рядом тенденций, выявленных на основании анализа исследований по проблемам обучения в сельских школах, результатов деятельности сельских школ в условиях современной социально-экономической ситуации, наблюдений практики обучения в них. Такими тенденц ...

Методика использования познавательной книги и рабочих тетрадей в логико-математическом развитии дошкольников
Обобщенный анализ данных позволяет выделить ряд требований к книге математического содержания. Книга должна: быть доступной по содержанию, представлениям и форме; соответствовать санитарно-гигиеническим требованиям (размер, используемые материалы и краски, качество и размер рисунков и т. п.); иметь ...