Электронное пособие по теме “Функциональные последовательности и ряды"

Решение

Так как , то при .

Ряд - мажорантный, исследуем его на сходимость. По признаку Даламбера имеем:

.

Так как , то ряд сходится. По теореме Вейерштрасса, так как для R , то заданный ряд сходится равномерно и абсолютно на промежутке .

Ответ: Заданный ряд сходится абсолютно и равномерно на интервале .

Пример №26 (№354 из [7]).

Исследовать на равномерную сходимость ряд на всей числовой оси.

Решение

Воспользуемся признаком Вейерштрасса равномерной и абсолютной сходимости функциональных рядов. Так как при любом , то справедливо неравенство , при R. - сходящийся ряд Дирихле с . Значит, и ряд сходится абсолютно и равномерно при R.

Ответ: Заданный ряд сходится абсолютно и равномерно при R.

Пример №27 (№76 из [10])

Показать, что ряд сходится равномерно на отрезке

Решение

Так как при 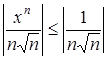, и ряд - сходящийся ряд Дирихле с , то, по признаку Вейерштрасса, ряд сходится абсолютно и равномерно на отрезке .

Ответ: Заданный ряд сходится абсолютно и равномерно на отрезке .

Пример №28 (№82 из [10]).

Сходится ли равномерно ряд , если ?

Решение

Если , то . Так как -сходящийся числовой положительный ряд - ряд Дирихле с , то по теореме Вейерштрасса, ряд сходится абсолютно и равномерно при .

Ответ: Заданный ряд сходится абсолютно и равномерно при .

Образование, педагогика, воспитание:

Понятие педагогической технологии
В педагогической и психологической литературе часто встречается понятие "технология", пришедшее к нам вместе с развитием компьютерной техники и внедрением новых компьютерных технологий. В педагогической науке появилось специальное направление - педагогическая технология. Это направление з ...

Дидактическая игра на уроке труда
Подготовка младших школьников к трудовой деятельности остается одной из основных и актуальных задач современной школы. Началом такой подготовки является формирование у учащихся интереса к труду и потребности овладеть определенными трудовыми умениями. Наиболее успешному осуществлению данной цели спо ...

Использование метода проектов при обучении информатике в начальной школе
Таким образом, раскрыв содержание понятий: «метод», «метод проектов», « проект», «учебная тема», «мышление», «младший школьный возраст» и выявив особенности метода проектов, мы пришли к выводу о том, что использование данного метода на уроках информатики способствует более эффективному усвоению уча ...